Previously we looked at a simple version of Rover’s overbooking problem. Once again, a disclaimer that this isn’t necessarily how Rover’s algorithm works, it’s just a framework that can help you think through how to solve this type of problem.
So let’s ratchet up the degree of difficulty by assuming that our dog sitters are in the following situation:
Jane: 7 requests, 2 vacancies, 40% booking rate (60% non-booking rate), $30 revenue per booked stay
Rob: 5 requests, 2 vacancies, 15% booking rate (85% non-booking rate), $30 revenue per booked stay
When we were working with sitters with single vacancies, we really only had to worry about the probability of absolutely none of the dog owners agreeing to book a stay. No matter what the number of inquiries was, there’s always only one way to get that outcome–same as, for example, there’s only one way to roll snake eyes with dice. For every other outcome where you have one or more agreeing to a stay, there are multiple ways of getting that combination–sticking to the previous example with dice, there are multiple ways of rolling a five or six or seven and so on with two dice.
As you probably didn’t come here looking for a rehash of your junior high or high school math, I’ll refer you to Wikipedia’s page on Pascal’s Triangle, particularly the section on Combinations. From there you’ll learn that you can get the number of ways to get 0, 1, 2, 3, 4, 5, 6, 7, or 8 people agreeing to a stay out of a set of 8 inquiries (Jane’s case, if we sent her the next lead). Where n = the number of inquiries and k is the number agreeing to a stay, use the following formula:

You learn that there are 1, 8, 28, 56, 70, 56, 28, 8, and 1 ways of getting 0, 1, 2, 3, 4, 5, 6, 7, or 8 people agreeing to a stay, respectively.
Now that we know how many combinations are possible, we have to find out the probability of getting one of those combinations.
The probability of 0 people booking a stay is 0.6^8 * 1. We multiply by 1 because there’s only one combination of 0 booked.
The probability of 1 person booking a stay is ((0.4^1) * (0.6^7)) * 8. We multiply by 8 at the end because there are 8 combinations booking.
The probability of 2 people booking a stay is ((0.4^2) * (0.6^6)) * 28. We multiply by 28 because there are 28 combinations of getting 2 people booking.
To avoid being too repetitive, you can generalize this as follows…
k = Number of People Booking A Stay — a variable that we will work through
n = Total Inquiries — 8 in Jane’s case
P(B) = Probability of Booking — 40% in Jane’s case
P(!B) = Probability of Not Booking — 60% in Jane’s case
C(n, k) = The number of combinations that result in “k” people booking a stay → n!/(k!(n – k)!)
Probability(k) = ((P(B)^n) * (P(!B)^(k – n)) * C(n, k)
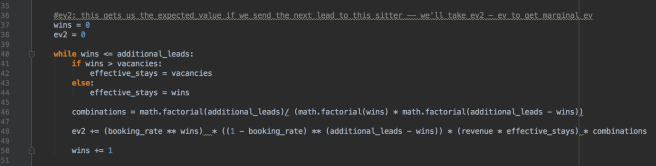
And from there we would calculate expected value (EV) by taking the probability of each combination and multiplying that by the revenue from that combination. So you’d get something like:
EV(0) = P(0) * $0 = 0.0168 * $0
EV(1) = P(1) * $30 = 0.0896 * $30
EV(2) = P(2) * $60 = 0.2090 * $60
EV(3) = P(3) * $60 = 0.2787 * $60 (Stays at $60 because Jane can only book a max of two stays)
EV(4) = P(4) * $60 = 0.2322 * $60
EV(5) = P(5) * $60 = 0.1239 * $60
EV(6) = P(6) * $60 = 0.0413 * $60
EV(7) = P(7) * $60 = 0.0079 * $60
EV(8) = P(8) * $60 = 0.0007 * $60
You would then add those all up to get your total expected value, which works out to about $56.30.
If we sent the next lead to Jane–who had 7 leads, but then would get bumped up to 8, her expected value would be $56.30.
Sending the next lead to Jane means not sending the next lead to Rob, so he stays at 5 leads. Running the same calculation for Rob, we find that his expected value is $21.63.
Adding up both Jane’s and Rob’s expected value gets us to ~ $77.94.
What about doing this the other way, where we send the next lead to Rob (bringing him to six leads) and not to Jane (leaving her at 7 leads)? A slightly higher expected value of approximately $79.79. In this scenario, it would be slightly better to steer the lead toward Rob rather than Jane.
These sorts of calculations for fairly static scenarios can be done somewhat easily in Excel, and hopefully I’ll get around to attaching some Excel files that you can use as a template. The real fun, however, is in being able to apply these lessons to an infinite number of scenarios. That’s going to be too tough of a job for Excel or SQL, however, so in the next post on this topic we’ll cover how to do this in Python.
(UPDATE: here’s Part 3 and how to do this in Python)